Задачи статистики в пакете SPSS
Диалоговое окно Р-Р Plots (Р-Р-диаграммы)
Рис. 22.62: Диалоговое окно Р-Р Plots (Р-Р-диаграммы)
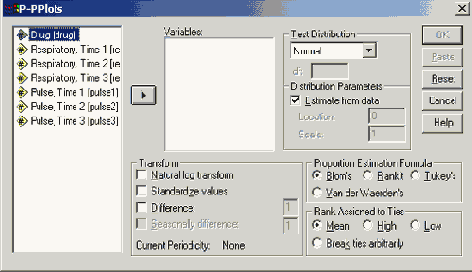
Вы видите, что тест на нормальное распределение устанавливается по умолчанию. Наряду с этим Вы можете производить тестирование на предмет наличия ещё двенадцати видов распределения, к примеру, на наличие распределения Вайбула (Weibull), Лапласа (Laplace), Хи-квадрат (%2) и /-распределения Стьюдента (Student). Вы можете просмотреть все предлагаемые типы распределений в ниспадающем меню.
-
Мы хотим проверить на предмет нормального распределения переменную а (Alter — возраст); для этого перенесите эту переменную в поле тестируемых переменных.
В диалоговом окне присутствуют также и различные возможности преобразования данных, в состав которых входят: пересчет в натуральные логарифмы, z-преобразование (перевод к стандартизованному виду) и два вида преобразований, применяемых для временных последовательностей.
Для подсчёта ожидаемых значений, подчиняющихся нормальному распределению, на выбор предлагаются четыре различных метода. Если количество значений, полученных в результате наблюдений, обозначить буквой п, а ранговые показатели этих значений буквой г (г = 1, ..., п), то формулы, соответствующие указанным методам, будут выглядеть следующим образом:
|
Blom (Блом): |
(r-3/8) / (n+1/4) |
|
Rankit (Ранговое преобразование): |
(r-1/2) / n |
|
Tukey (Тьюки): |
(r-1/З) / (n+1/З) |
|
Van der Waerden (Ван дер Верден): |
r / (n+1) |
Формула Блома (Blom) устанавливается по умолчанию. Далее Вам предоставляется возможность выбора одного из четырёх различных методов для обозначения одинаковых значений (так называемых связок).
|
Среднее значение: |
Равным значениям присваивается средний ранг |
|
Максимум: |
Равным значениям присваивается ранг, высший из двух |
|
Минимум: |
Равным значениям присваивается ранг, низший из двух |
|
Связи разрывать произвольно |
Если в первых трёх методах для дельнейшего анализа используется только один элемент данных, то в этом методе может использоваться столько элементов, сколько значений имеется в наличии. |
-
Оставьте предварительные установки и подтвердите построение диаграммы нажатием ОК.
Будут построены две диаграммы. На первой, простой Р-Р-диаграмме отображается зависимость ожидаемых совокупных частот от фактических совокупных частот, рассчитанная при помощи формулы рангового преобразования Блома (Blom). На второй диаграмме, Р-Р-диаграмме без тренда, отображается разность между фактическими и ожидаемыми совокупными (кумулятивными) частотами в зависимости от фактических совокупных частот.
