Диалоговое окно Reliability Analysis'.Statistics (Анализ пригодности: Статистики)

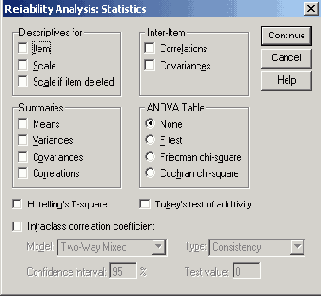
Scale if item deleted (Масштабировать, если пункт удалён): Когда при расчёте значения масштаба этот пункт (вопрос) не учитывается, для каждого такого Пункта (ответа на вопрос анкеты), выводятся: среднее значение и дисперсия значения шкалы, корреляция пункта со значением масштаба (то есть избирательность) и альфа Кохрана.

Summaries (Итоги, общие сведения)

Means (Средние значения): Различные виды статистик для средних значений пунктов

Variances (Дисперсия): Различные виды статистик для дисперсий пунктов

Covariances (Ковариации): Различные виды статистик для ковариаций между пунктами

Correlations (Корреляции): Различные виды статистик для корреляций между пунктами.

Inter-Item (Между пунктами)

Correlations (Корреляции): Корреляционная матрица Covariances (Ковариации): Ковариационная матрица

ANOVA-ТаЫе (Таблица ANOVA)

F test (F тест): Двухфакторный дисперсионный анализ (факторы: наблюдения, пункты) с повторным измерением и одним значением в каждой ячейке Friedman chi-square (Хи-квадрат Фридмана): тест Хи-квадрат Фридмана и коэффициент согласования Кендала (при наличии переменных, относящихся к порядковой шкале)

Cochran chi-square (Хи-квадрат Кохрана): Q Кохрана (при наличии дихотомических переменных).

Далее ещё имеются:

Hottelling's T-square (Т-квадрат Хоттелинга): Тест Хоттелинга для проверки утверждения, что средние значения пунктов равны между собой.
Tukey's test ofadditivity (Критерий аддитивности Тьюки): Тест Тьюки на аддитивность пунктов.

В случае установки опции Intraclass correlation coefficient (Корреляционный коэффициент внутри класса) речь идёт о расчёте корреляционного коэффициента внутри класса (ICC); информацию по этому поводу Вы найдёте в разделе 15.5.

Здесь ограничьтесь активизацией опции Scale if item deleted (Масштабировать, если пункт удалён) и щёлкните на Continue (Далее).
Начните расчёт нажатием ОК.

В окне просмотра появятся результаты расчёта. И в 10 версии вывод этих результатов ещё не производится в новой табличной форме.

RЕLIАВILIТУ ANALYSIS SCALE (ALPHA)
Item-total	Statistics
	Scale Mean if Item Deleted	Scale Variance if Item Deleted	Corrected Item-Total Correlation	Alpha if Item Deleted
ITEM1	24,9333	13,5126	,5410	,7664
ITEM2	25,0667	14,4092	,2679	,7862
ITEM3	25,1000	13,5414	,5097	,7684
ITEM4	25,4333	16,0471 -	-,1676	,8052
ITEMS	25,2000	13,6828	,4907	,7701
ITEM6	25,1667	14,5575	,2358	,7883
ITEM7	25,5000	15,2931	,1738	,7887
ITEMS	24,8000	15,1310	,1154	,7942
ITEM9	25,2000	13,8897	,4304	,7745
ITEM10	24,8667	13,8437	,4732	,7717
ITEM11	25,3667	14,2402	,4223	,7760
ITEM12	25,0667	13,3057	,5763	,7633
ITEM13	25,0000	13,2414	,6017	,7615
ITEM14	24,9667	13,8954	,4196	,7752
ITEM15	25,0000	13,3103	,5813	,7630
ITEM16	25,0333	14,0333	,3713	,7787
ITEM17	24,9667	15,3437	,0283	,8023
ITEM18	24,9667	13,9644	,4000	,7766
Reliability Coefficients
N of Cases =30,0			N of Items= 18
Alpha =,7887

Коэффициент пригодности, равный 0,7887, является очень высоким. В колонке с названием Corrected Item-Total Correlation (Откорректированный пункт — суммарная корреляция) находятся коэффициенты избирательности. Основываясь на значении этих коэффициентов, пункты 4 и 17 можно считать непригодными для дальнейшего использования, да и пункт 8 должен быть исключён.

Мы уже говорили о необходимости проведения расчета индекса сложности. Для расчёта индекса сложности выберите в меню Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Frequencies... (Частоты)

Процентный показатель частоты появления правильного ответа (кодировка 1) является индексом сложности соответствующего пункта. Все индексы сложности собраны в нижеследующей таблице.

Пункт	Индекс сложности	Пункт	Индекс сложности
1	36,7	10	30,0
2	50,0	11	80,0
3	53,3	12	50,0
4	86,7	13	43,3
5	63,3	14	40,0
6	60,0	15	43,3
7	93,3	16	46,7
8	23,3	17	40,0
9	63,3	18	40,0

Если следовать рекомендации, сформулированной в начале раздела и исключать пункты с индексом сложности меньшим 20 и большим 80, то помимо пунктов 4, 8 и 17 необходимо исключить из списка и пункт 7.

Если вновь провести анализ пунктов с оставшимися четырнадцатью пунктами, то коэффициент пригодности получится равным 0,8297. Благодаря исключению неподходящих пунктов он стал ещё выше.

Содержание раздела