Задачи статистики в пакете SPSS
Диалоговое окно Variance Components (Компоненты дисперсии)
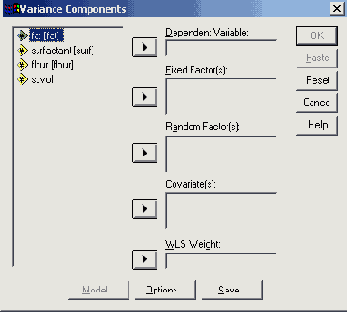
Диалоговое окно Variance Components (Компоненты дисперсии)
В окне просмотра появятся оценки компонентов дисперсии.
Factor Level Information (Информация о слоях фактора)
|
|
N | |
|
PFLANZE (Растение) |
1,00 |
6 |
|
2,00 |
4 | |
|
3,00 |
5 | |
Dependent Variable: LAENGE (Зависимая переменная: Длина)
Variance Estimates (Оценки дисперсии)
|
Component (Компоненты) |
Estimate (Оценка) |
|
Var(PFLANZE) (Переменная (Растение)) |
,471 |
|
Var(Error) (Переменная (Ошибка)) |
,438 |
Dependent Variable: LAENGE (Зависимая переменная: Длина) Method: Minimum Norm Quadratic Unbiased Estimation (Weight = 1 for Random Effects and Residual) (Метод: Минимум нормы квадратичной несмещённой оценки (Вес = 1 для случайных эффектов и остатков))
На основе этих результатов можно найти процентную долю дисперсии, получающуюся из-за наличия разных растений:
0,471/(0,471+0,438)=51,8%
Приведём ещё один несколько усложненный пример из учебника SPSS. На некоторой фирме, работающей в области электроники, в 36 различных печах при различных температурах (550 и 600 градусов по Фаренгейту) измеряют выносливость (в минутах) определенных радиоэлектронных комплектующих. Один инженер предполагает, что не все печи создают одинаковые условия для тестирования комплектующих. Чтобы это проверить, он случайно выбирает три печи и для каждой печи делает по три измерения выносливости комплектующих для каждой из температур.
Данные находятся в файле ofen.sav в переменных of en (печь), temp (температура) и zeit (время). Переменная ofen (печь) соответствует фактору со случайными эффектами, так как из 36 печей три были выбраны случайно. Температура также является фактором со случайными эффектами, так как температуры 550 и 600 градусов были выбраны из бесконечного множества возможных температур.
Так как вполне возможно, что в разных печах действуют различные температурные режимы, предположим, что температурный фактор является вложенным в фактор печей — т.н. ("гнездовая компоновка'").
-
Откройте файл ofen.sav.
-
Откройте так, как было изложено ранее, диалоговое окно Variance Components (Компоненты дисперсии).
-
Переменную zeit (время) поместите в поле зависимых переменных, а переменные ofen (печь) и temp (температура) в поле случайных факторов.
Мы должны здесь также учесть и вложенность фактора temp (температура) в фактор ofen (печь). Это можно осуществить только при помощи программного синтаксиса.
-
Щёлкните по выключателю Paste (Внести) для того, чтобы перенести синтаксис данной команды в редактор синтаксиса.
В редакторе будет показан следующий синтаксис:
VARCOMP
zeit BY ofen temp
/RANDOM = ofen temp
/METHOD = MINQUE (1)
/DESIGN
/INTERCEPT = INCLUDE .
-
Дополните вспомогательную команду DESIGN следующим образом:
VARCOMP
zeit BY ofen temp
/RANDOM = ofen temp
/METHOD = MINQUE (1)
/DESIGN = ofen temp(ofen)
/INTERCEPT = INCLUDE .
-
Запустите команду на исполнение при помощи кнопки Run Current. В окне просмотра появятся следующие оценки дисперсии:
Variance Estimates (Оценки дисперсии)
|
Component (Компонент) |
Estimate (Оценка) |
|
Var(OFEN) (Переменная (Печь)) |
29,287 |
|
Var(TEMP(OFEN)) (Переменная Температура (Печь)) |
1525,889 |
|
Var(Error) (Переменная (Ошибка)) |
69,778 |
Dependent Variable: ZEIT (Зависимая переменная: Время) Method: Minimum Norm Quadratic Unbiased Estimation (Weight = 1 for Random Effects and Residual) (Метод: Минимум нормы квадратичной несмещённой оценки (Вес = 1 для случайных эффектов и остатков))
Из таблицы можно узнать, что доля дисперсии объясняемая наличием разных печей очень незначительна:
[29, 287/(29,287 + 1525,889 + 69,778)]*100 = 1,8%
До этого момента мы рассматривали только модели со случайными эффектами. Модели, содержащие как случайные, так и постоянные эффекты, получили название "смешанных" моделей.
И, наконец, следует указать на то, что методы MINQUE и ANOVA иногда могут выдавать негативные оценки компонентов дисперсии, что собственно противоречит самому определению дисперсии. Это может происходить потому, что количество наблюдений слишком мало, некоторые значения отсутствуют или выбран неподходящий метод оценки.
Содержание раздела
