Задачи статистики в пакете SPSS
Диалоговое окно Univariate: Post...
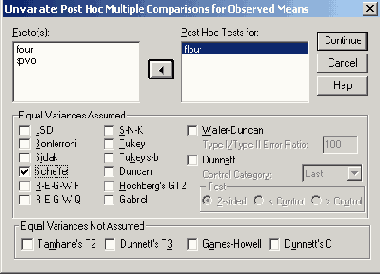
Диалоговое окно Univariate: Post Hoc Multiple Comparisons for Observed Means (Одномерная: Дополнительно — многократные сравнения для наблюдаемых средних значений)
Between-Subjects Factors (Межсубъектные факторы)
|
|
|
Value Label (Метка значения) |
N |
|
GESCHL (Пол) |
1 |
maennlich (Мужской) |
15 |
|
2 |
weiblich (Женский) |
12 | |
|
ALTER (Возраст) |
1 |
bis 30 Jahre (До 30 лет) |
7 |
|
2 |
31 - 50 Jahre (31 - 50 лет) |
9 | |
|
3 |
ueber 50 Jahre (Свыше 50 лет) |
11 |
Descriptive Statistics (Дескриптивные статистики)
|
Dependent Variable: М1 (Зависимая переменная: М1) | ||||
|
GESCHL ' (Пол) |
ALTER (Возраст) |
Mean (Среднее значение) |
Std. Deviation (Стандартное отклонение) |
N |
|
maennlich (Мужской) |
bis 30 Jahre (До 30 лет) |
16,00 |
,82 |
4 |
|
31 - 50 Jahre (31 - 50 лет) |
14,60 |
1,14 |
5 | |
|
ueber 50 Jahre (Свыше 50 лет) |
11,7 |
2,48 |
6 | |
|
Total (Сумма) |
13,60 |
2,69 |
15 | |
|
weiblich (Женский) |
bis 30 Jahre (До 30 лет) |
16,00 |
1,00 |
3 |
|
31 - 50 Jahre (31 - 50 лет) |
15,00 |
1,41 |
4 | |
|
ueber 50 Jahre (Свыше 50 лет) |
10,20 |
1,10 |
5 | |
|
Total (Сумма) |
13,25 |
2,93 |
12 | |
|
Total (Сумма) |
bis 30 Jahre (До 30 лет) |
16,00 |
,82 |
7 |
|
31 - 50 Jahre (31 - 50 лет) |
14,78 |
1,20 |
9 | |
|
ueber 50 Jahre (Свыше 50 лет) |
10,73 |
1,95 |
11 | |
Levene's Test of Equality of Error Variances a (Тест Левене на равенство дисперсии ошибок)
Dependent Variable: М1 (Зависимая переменная: М1)
|
F |
df1 |
df2 |
Sig(Значимость) |
|
4,177 |
5 |
21 |
,009 |
Tests the null hypothesis that the error variance of the dependent variable is equal across groups (Проверяет нулевую гипотезу о том, что дисперсия ошибок зависимых переменных одинакова для всех групп).
a. Design: Intercept+GESCHL+ALTER+GESCHL * ALTER (Компоновка: Отрезок + Пол + Возраст + Пол*Возраст)
К сожалению, тест Левене на равенство дисперсий показывает, значимый результат со значением вероятности ошибки р = 0,009. Это означает, что отсутствует однородность дисперсий между группами, которая наряду с нормальным распределением значений выборки, является основной предпосылкой для возможности проведения дисперсионного анализа.
Традиционная схема дисперсионного анализа (еще раз отметим: проводимого на основе общей линейной модели) показывает незначимое влияние пола (р = 0,761), очень значимое влияние возраста (р = 0,001) и незначимое взаимодействие между обоими переменными (р = 0,611).
Tests of Between-Subjects Effects (Тест межсубъектных эффектов)
Dependent Variable: M1 (Зависимая переменная: М1)
|
Source (Источник) |
Type III Sum of Squares (Сумма квадратов III типа) |
Df |
Mean Square (Среднее значение квадрата) |
F |
Sig. (Значи-мость) |
|
Corrected Model (Подпра- вленная модель) |
145,833a |
5 |
29,167 |
12,049 |
,000 |
|
Intercept (Отрезок) |
4916,763 |
1 |
4916,763 |
2031,187 |
,000 |
|
GESCHLJOonl |
,229 |
1 |
,229 |
,095 |
,761 |
|
ALTER (Возраст) |
144,273 |
2 |
72,137 |
29,801 |
,000 |
|
GESCHL * ALTER (Пол'Возраст) |
2,446 |
2 |
1,223 |
,505 |
,611 |
|
Error (Ошибка) |
50,833 |
21 |
2,421 |
|
|
|
Total (Сумма) |
5077,000 |
27 |
|
|
|
|
Corrected Total |
196,667 |
26 |
|
|
|
a R Squared = ,742 (Adjusted R Squared = ,680) (R-квадрат = 0,742 (смещённый R-квадрат = 0,680))
В случае отсутствия однородности дисперсии границу значимости рекомендуется устанавливать равной не р = 0,05, а р =0,01. Значимое влияние возраста проявляется в любом случае.
Если вы сравните эти результаты с результатами, полученными при методе Фишера (Fisher) (см. гл. 17.1.2), то заметите незначительное отклонение значения р для фактора влияния пол (geschlecht). Далее следует вывод дескриптивных статистик для совокупной выборки и для отдельных слоев факторов.
1. Grand Mean (Общее среднее значение)
| Dependent Variable: М1 (Зависимая переменная: М1) | |||
|
Mean (Среднее значение) |
Std. Error (Стандартная ошибка) |
95% Confidence Interval (95 % доверительный интервал) | |
|
Lower Bound (Нижний предел) |
Upper Bound (Верхний предел) | ||
|
13,828 |
,307 |
13,190 |
14,466 |
2. GESCHL (Пол)
| Dependent Variable: М1 (Зависимая переменная: М1) | ||||
|
GESCHL (Пол) |
Mean (Среднее значение) |
Std. Error (Стандартная ошибка) |
95% Confidence Interval (95 % доверительный интервал) | |
|
Lower Bound (Нижний предел) |
Upper Bound (Верхний предел) | |||
|
maennlich (Мужской) |
13,922 |
,407 |
13,075 |
14,769 |
|
weiblich (Женский) |
13,733 |
,459 |
12,779 |
14,688 |
3. ALTER (Возраст)
| Dependent Variable: М1 (Зависимая переменная: М1) | ||||
|
ALTER (Возраст) |
Mean (Среднее значение) |
Std. Error (Стандартная ошибка) |
95% Confidence Interval (95 % доверительный интервал) | |
|
Lower Bound (Нижний предел) |
Upper Bound (Верхний предел) | |||
|
bis 30 Jahre (До 30 лет} |
16,000 |
,594 |
14,764 |
17,236 |
|
31 - 50 Jahre (31 - 50 лет) |
14,800 |
,522 |
13,715 |
15,885 |
|
ueber 50 Jahre (Свыше 50 лет) |
10,683 |
,471 |
9,704 |
11,663 |
Затем следует вывод результатов теста Шеффе по сравнению отдельных возрастных групп. На основании частично дублированных результатов, можно сделать вывод, что самая старшая возрастная группа очень значимо отличается от двух других:
Multiple Comparisons (Множественные сравнения)
| Dependent Variable: M1 (Зависимая переменная: М1) Scheffe (Шеффе) | ||||||
|
(I) ALTER (Возраст) |
(J) ALTER (Возраст) |
Mean Difference (I-J) (Средняя разность) |
Std. Error (Стандар -тная ошибка) |
Sig. (Значи-мость) |
95% Confidence Interval (95 % доверительный интервал) | |
|
Lower Bound (Нижний предел) |
Upper Bound (Верхний предел) | |||||
|
bis 30 Jahre (До 30 лет) |
31 -50 Jahre (31 -50 лет) |
1,22 |
,784 |
,317 |
-.84 |
3,29 |
|
ueber 50 Jahre (Свыше 50 лет) |
5,27* |
,752 |
,000 |
3,29 |
7,25 | |
|
31 -50 Jahre (31 -50 лет) |
bis 30 Jahre (До 30 лет) |
-1,22 |
,784 |
,317 |
-3,29 |
,84 |
|
ueber 50 Jahre (Свыше 50 лет) |
4,05* |
,699 |
,000 |
2,21 |
5,89 | |
|
ueber 50 Jahre (Свыше 50 лет) |
bis 30 Jahre (До 30 лет) |
-5,27* |
,752 |
,000 |
-7,25 |
-3,29 |
|
31 -50 Jahre (31 -50 лет) |
-4,05* |
,699 |
,000 |
-5,89 |
-2,21 | |
Based on observed means (Основываясь на наблюдаемых средних значениях). * The mean difference is significant at the ,05 level (Усреднённая разность является значимой на уровне 0,05).
Этот факт подтверждается ещё раз при выводе результатов для рассматриваемых "однородных подгрупп" в другой форме.
М1
| Scheffe аbс (Шеффе) | |||
|
ALTER |
N |
Subset (Подгруппа) | |
|
1 |
2 | ||
|
ueber 50 Jahre (Свыше 50 лет) |
11 |
10,73 |
|
|
31 - 50 Jahre (31 - 50 лет) |
9 |
|
14,78 |
|
bis 30 Jahre (До 30 лет) |
7 |
|
16,00 |
|
Sig. (Значимость) |
|
1,000 |
,283 |
Means for groups in homogeneous subsets are displayed (Выводятся средние значения для групп в однородных подгруппах).
Based on Type III Sum of Squares (На основе суммы квадратов III типа).
The error term is Mean Square(Error) = 2,421 (Слагаемое ошибки равно среднему значению квадрата (ошибки) = 2,421).
a. Uses Harmonic Mean Sample Size = 8,699 (Используя среднегармонический размер выборок = 8,699).
b. The group sizes are unequal (Размеры групп не одинаковы). The harmonic mean of the group sizes is used (Используется среднее гармоническое размера групп). Туре I error levels are not guaranteed (Уровень ошибки для I типа не гарантируется).
с. Alpha = ,05
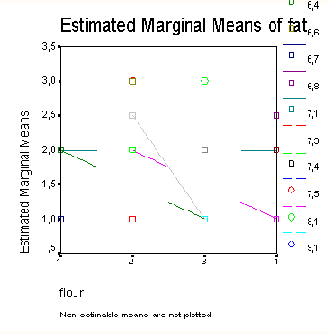
Завершает вывод результатов профильная диаграмма, в которой представлена линейчатая диаграмма возраста отдельно для каждого пола:
Вид графиков для обоих полов почти одинаков, что свидетельствует о незначимом взаимодействии между двумя факторами. Кроме того, наглядно проявляется незначимость различия между двумя полами.
Содержание раздела
