Диалоговое окно Univariate: Model (Одномерная: Модель)

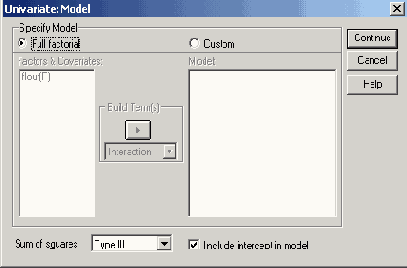
Модель дисперсионного анализа — это математическое соотношение, в котором каждая переменная представлена в виде суммы среднего значения и ошибки. Что касается выбора конкретной формы модели, то по умолчанию установлена полнофакторная модель Full factorial). В этой модели среднее значение каждого наблюдения представлено в виде генерального среднего и суммы вклада всех главных "эффектов" (факторов влияния), помимо которых производится также расчёт всех взаимодействий между факторами. Альтернативой является возможность выбора отдельных взаимодействий факторов влияния, которая осуществляется посредством активирования опции Custom (Пользовательский режим). Таким же образом должны быть отобраны и взаимодействия с ковариациями.

Для формирования сумм квадратов для МНК существует четыре различных подхода (четыре типа, обозначенных с помощью римских чисел I, II, III и IV), по умолчанию установлен тип III.

Оставьте в этом окне все установки по умолчанию и покиньте диалоговое окно нажатием кнопки Continue (Далее).
Щёлкните на выключателе Options... (Опции)

Откроется диалоговое окно Univariate: Options (Одномерная: Опции) (см. рис. 17.4)

Перенесите OVERALL (В целом) и обе переменные geschl (пол) и alter (возраст) в поле Display means for (Показать средние значения для); в этом случае в качестве результатов будут выведены средние значения и стандартная ошибка для совокупной выборки (OVERALL) и для всех слоев по обоим факторам. Средние значения для комбинаций взаимодействия на этом этапе рассчитываются только для неполнофакторных моделей.

Затем активируйте Descriptive Statistics (Дескриптивные статистики); благодаря выбору этой опции выводятся среднее значение, стандартные отклонения и количество наблюдений во всех ячейках.
Активируйте затем опцию Homogeneity tests (Тесты на однородность). Таким образом активируется проверка однородности дисперсии. Покиньте диалоговое окно нажатием Continue (Далее).
При помощи выключателя Plots... (Диаграммы) откройте диалоговое окно Univariate: Profile Plots (Одномерная: Профильные диаграммы) (см. рис. 17.5).

Содержание раздела