Задачи статистики в пакете SPSS
Диаграмма рассеяния
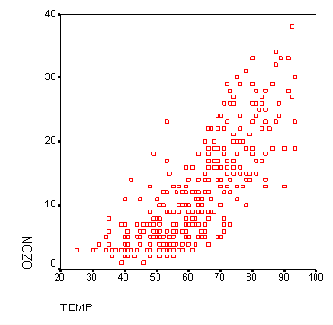
Рис. 16.26: Диаграмма рассеяния
-
Отметьте и постройте простую диаграмму рассеяния с переменной alter по оси абсцисс и переменной staedte пo оси ординат.
Вы увидите, что с ростом возраста растёт не только количество названных городов, но и рассеяние, то есть дисперсия, становится больше.
-
В соответствии с описанием из главы 16.1 проведите линейный регрессионный анализ, причём переменной staedte присвойте статус зависимой переменной, а переменной alter — независимой переменной.
-
Вы получите следующие результаты:
Model Summary (Сводная таблица по модели)
|
Model (Модель) |
R |
R Square (R-квадрат) |
Adjusted R Square (Смещенный R-квадрат) |
Std. Error of the Estimate (Стандартная ошибка оценки) |
|
1
|
,879а |
,772 |
,766
|
3,1623 |
a. Predictors: (Conslant), Alter (Bлияющие переменные: (Константа), возраст)
|
Coefficients (Коэффициенты) а | ||||||
|
Model (Модель) |
Unstandardized Coefficients (He стандарти-зированные коэф-фициенты) |
Standardized Coefficients (Стандарти-зированные коэф-фициенты) |
Т |
Sig. (Значи-мость) | ||
|
В |
Std. Error (Станда-ртная ошибка) |
/3 (Beta) | ||||
|
1 a. Dep |
(Constant) (Koнстанта) |
-2,722 |
1,273 |
|
-2,138 |
,039 |
|
Alter (Возраст) endent Variable |
1,569 (Зависим |
,138 ая перемен-ная) |
,879 |
11,357 |
,000 | |
Коэффициент корреляции равен 0,879, а мера определённости 0,772.
В данном примере мы имеем дело с группами случаев, разделёнными по годам возраста, для которых независимая переменная имеет всегда одно и то же значение. Исходя из значений зависимой переменной сопоставленных каждому случаю, можно определить дисперсию; обратное значение этой дисперсии применяется обычно в качестве весового фактора для соответствующего случая.
Если подобной группировки данных нет, то пытаются выявить такую связь между дисперсией и переменной, чтобы степень дисперсии была пропорциональна значению данной переменной. При поиске так называемых весовых переменных речь идет о независимой переменной или, если их много, — об одной из независимых переменных. В приведенном примере такой переменной, очевидно, является независимая переменная alter, по которой и можно проследить изменение дисперсии.
Целью анализа сначала является определение наилучшей возможной степени р. а затем подсчёт веса для каждого случая, причём вес для значения переменной х определяется как
1/хp
-
Выберите в меню Analyze (Анализ) Regression.. .(Регрессия) Weight Estimation... (Взвешенное оценивание)
Откроется диалоговое окно Weight Estimation (Взвешенное оценивание).
