Задачи статистики в пакете SPSS
Диаграммы рассеяния
Рис. 15.1.Диаграммы рассеяния
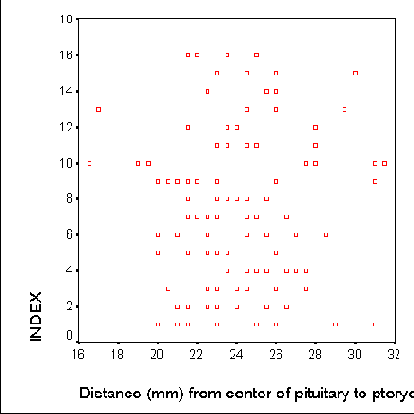
Если коэффициент корреляции отрицательный, это означает наличие противоположной связи: чем выше значение одной переменной, тем ниже значение другой. Сила связи характеризуется также и абсолютной величиной коэффициента корреляции. Для словесного описания величины коэффициента корреляции используются следуюшие градации:
|
Значение |
Интерпретация |
|
до 0,2 |
Очень слабая корреляция |
|
до 0,5 |
Слабая корреляция |
|
до 0,7 |
Средняя корреляция |
|
до 0,9 |
Высокая корреляция |
|
свыше 0,9 |
Очень высокая корреляция |
Метод вычисления коэффициента корреляции зависит от вида шкалы, которой относятся переменные.
-
Переменные с интервальной и с номинальной шкалой: коэффициент корреляции Пирсона (корреляция моментов произведений).
-
По меньшей мере, одна из двух переменных имеет порядковую шкалу либо не является нормально распределённой: ранговая корреляция по Спирману или т (тау-грого-соая) Кендала.
-
Одна из двух переменных является дихотомической: точечная двухрядная корреляция. Эта возможность в SPSS отсутствует. Вместо этого может быть применён расчёт ранговой корреляции.
-
Обе переменные являются дихотомическими: четырёхполевая корреляция. Данный вид корреляции рассчитываются в SPSS на основании определения мер расстояния и мер сходства (см. гл 15.4).
Расчёт коэффициента корреляции между двумя недихотомическими переменными не лишён смысла только тогда, кода связь между ними линейна (однонаправлена). Если связь, к примеру, U-образная (неоднозначная), то коэффициент корреляции непригоден для использования в качестве меры силы связи: его значение стремится к нулю. В следующих разделах будут рассмотрены корреляции по Пирсону, Спирману и Кендалу. Ешё один раздел специально посвящён частной корреляции.
Содержание раздела
