Диалоговое окно Independent-Samples T Test

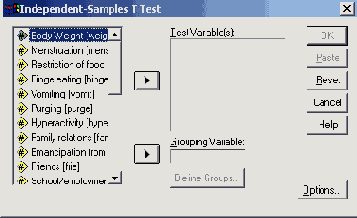
Запустите t-тест, щелкнув на ОК. В окне просмотра появятся следующие результаты:

Group Statistics (Статистика групп)

	Лекарство	N	Mean (Среднее)	Std. Deviation (Стандартное отклонение)	Std. Error Mean (Стандартная ошибка среднего)
Возраст	Альфасан	87	62,24	11,19	1,20
Возраст	Бетасан	87	61,98	11,96	1,28

Independent Samples Test (Тест для независимых выборок)

		Levene's Test for Equality of Variancies (Тест Левена на равенство дисперсий)		t-test for Equality of Means (Тест Стьюдента на равенство средних)
		F	Sig. (Значи-мость)	Т	df	Sig. (2-tailed) (Значимость (двусто- ронняя))	Mean Diffe-rence (Разность средних)	Std. Error Differe-псе (Станда- ртная ошибка разницы)	95 % Confidence Interval of the Difference (Довери-тельный интервал разницы)
Lower (Нижняя граница)	Upper (Верхняя граница)
Возраст	Equal variances assumed (Дис-персии равны)	,54	,462	,151	172	,880	,26	1,76	-3,20	3,73
	Equal variances not assumed (Ди- сперсии не равны)			,15'	171,249	,880	,26	1,76	-3,20	3,73

Выведенные результаты содержат:

количество наблюдений, средние значения, стандартные отклонения и стандартные ошибки средних в обеих группах,
результаты теста Левена на равенство дисперсий.

Как правило, гипотеза о равенстве (гомогенности) дисперсий не принимается, если тест Левена дает значение р < 0,05 (гетерогенность дисперсий). Для случаев как гомогенности (равенства), так и гетерогенности (неравенства) выводятся следующие характеристики:

результаты t-теста: значение распределения t, количество степеней свободы df, вероятность ошибки р (под обозначением "Значимость (2-сторонняя)"), а также
разница средних значений, ее стандартная ошибка и доверительный интервал.

В данном примере мы не получаем значимого различия воздействия двух группами лекарств по возрасту (р = 0,880).

В следующем t-тесте мы проверим, различается ли действие двух групп лекарств по так называемому индексу Брока. Этот индекс, разработанный одним парижским хирургом, предусматривает, что нормальный вес человека можно определить из следующего уравнения:

Нормальный вес (кг) = Рост (см) — 100

Если взять отношение фактического веса человека к нормальному весу по этой рормуле, то мы получим процентный показатель, который у людей с нормальным весом равен 100, у людей с избытком веса > 100 и т.д.

Индекс Брака =((Вес в кг)/(Рост в см - 100)) • 100

Определим на основе существующих переменных новую переменную, для чего выберем команды меню Transform (Преобразовать) Compute... (Вычислить)
В поле выходной переменной (Target Variable) задайте новое имя "broca", а в поле численного выражения (Numeric Expression) введите выражение gew I (gr- 100) * 100
Щелкните на кнопке ОК. Теперь можно командами меню Analyze (Анализ) Compare Means (Сравнение средних) Independent Samples T Test... (t-тест для независимых выборок) описанным выше способом провести t-тест для новой переменной broca.

И этот тест показывает, что между двумя труппами лекарств не наблюдается значимого различия по индексу Брока (р = 0,233).

Содержание раздела