Гистограмма возрастной структуры

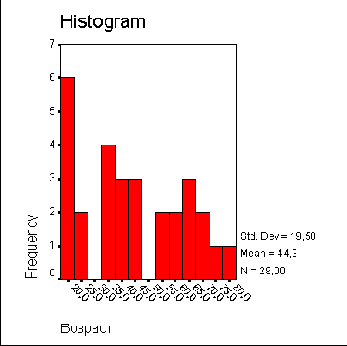
Далее мы посмотрим, какие результаты можно получить, если установить в диалоговом окне Explore: Plots флажок Normality plots with tests (Диаграмма нормального распределения с тестами).

Установите этот флажок и подтвердите настройку кнопкой ОК.

В окне просмотра будет показан результат теста Лиллифора (модификации теста Колмогорова-Смирнова) на нормальное распределение.

Если в результате получена вероятность ошибки р менее 0,05, то данное распределение значимо отличается от нормального. В данном примере при р = 0,200 распределение можно считать нормальным. При объеме выборки менее 50 наблюдений проводится также тест Шапиро-Уилкса.

Tests of Normality (Тесты на нормальное распределение)

	Kolmoqorov-Smirnov (а) (Колмогоров-Смирнов)
Statistic	df	Sig.
Возраст	,059	174	,200*

*. This is a lower bound of the true significance (Это нижняя граница истинной значимости), a. Lilliefors Significance Correction (Коррекция значимости по Лиллифору).

В окне просмотра будут показаны две диаграммы:

диаграмма нормального распределения
диаграмма с исключенным трендом

По диаграмме нормального распределения (также называемой диаграммой Q-Q) можно визуально определить, достаточно ли близко заданное распределение приближается к нормальному. Здесь каждое наблюдаемое значение сравнивается со значением, ожидаемым при нормальном распределении. При условии точного выполнения нормального распределения все точки лежат на прямой. Наблюдаемые значения откладываются по оси X, а ожидаемые — по оси Y, при этом все значения подвергаются стандартизации (z-преобразованию). В данном примере (см. рис. 10.6) наблюдаемые значения достаточно близки к прямой.

Содержание раздела